Дисциплина
«МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ.»
Содержание комплекта:
1. Список студентов группы №
2. Методические указания для выполнения первого контрольного домашнего задания по теме «Идентификация формы закона распределения погрешностей».
3. Перечень вопросов для самоподготовки по дисциплине «Метрология, стандартизация и сертификация».
4. Варианты заданий для расчетно-графических работ (контрольных домашних работ) по дисциплине «Метрология, стандартизация и сертификация».
Указание:
1. № варианта задания выбирается в соответствии с порядковым номером студента в списке группы.
2. Комплект хранится в деканате филиала до начала экзаменационной сессии.
1.4.2.Идентификация
формы закона распределения погрешностей.
(построение
гистограммы) [1, 119;2, 65]
Экспериментальные
исследования погрешностей средств измерений различных типов показали, что
существует много законов распределения погрешностей, причем часто они
существенно отличаются от гауссовского. Поскольку знание реального закона распределения
необходимо для выбора методики получения оценки измеряемой величины, то в
необходимых случаях приходится выбирать закон распределения, в наибольшей мере
соответствующей эксперимсентальным данным – идентифицировать форму закона
распределения. Исходные данные для выбора закона распределения получают из гистограммы,
т.е. экспериментально построенного графика статистического распределения
погрешностей.
Пример 1.6. Произвести
статистическую обработку ряда наблюдений измеряемой величины X1 ; X 2 ; X
3; ·
· · X n-1 ; X n . Выявить и исключить
промахи в результатах наблюдений. Определить значение результата измерения,
предполагая отсутствие систематической погрешности, с учетом малого числа
измерений одной и той же физической величины (использовать при этом критерий
Стъюдента). Определить случайную среднеквадратическую погрешность среднеарифметических
значений серии измерений
Построить гистограмму результатов наблюдений.
Решение:
1.Исключаем из заданного
ряда наблюдений грубые ошибки – промахи. Для этого найдём:
а). среднеарифметическое
значение (матожидание) результатов наблюдения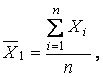 
(1.17)
где n –
общее число наблюдений;
б). абсолютные
погрешности каждого наблюдения 
(1.18)
в). среднеквадратическое
значение (СКО) одного ряда измерения 
(1.19)
г).обнаруживаем грубую
ошибку (промах) по критерию xi> 3σ1 и исключаем этот(и)
результат(ы) из ряда измерений;
Примечание: Следует обратить
внимание, что критерий 3σ справедлив для заданной доверительной
вероятности P = 0,997, если доверительная
вероятность P = 0,95,то критерий равен 2σ,
а при P = 0,9 − критерий равен 1,65σ.
Если в условии задачи
доверительная вероятность не задана, то её следует самостоятельно принять равной
0.997.
д).на основании
оставшегося ряда измерений повторно определяем 
и проверяем на наличие
промаха. И так до тех пор, пока не будут исключены все грубые ошибки, при этом
каждый раз определяем 
2.Из оставшихся
результатов наблюдения выстраиваем вариационный ряд, т.е.
располагаем результаты в прядке возрастания их значений и выбираем минимальное 
и максимальное 
значения – крайние
члены вариационного ряда.
3.Разбиваем вариационный
ряд на r – число равных интервалов – бинов. Число
интервалов r определяется числом измерений n и может быть выбрано на
основании табл. №1.2., рекомендованной ВНИИМ [9, 120].
Таблица №1.2. 4.Ширина
бинов определяется по формуле
|
n |
r |
|
< 30 |
5 – 8 |
|
30 – 100 |
7 – 9 |
|
100 – 500 |
8 – 12 |
|
500 – 1000 |
10 – 16 |
|
1000 – 10000 |
12 – 22 |
, (1.20)
Следует соблюдать некоторую
осторожность при выборе ширины бинов 
для гистограммы. Если
бины выбрать слишком широкими, то все
(или почти все) отсчеты попадут в один бин и гистограмма выродится в
малоинтересный единственный прямоугольник. Если же бины выбраны слишком узкими
, то лишь небольшое их число будет содержать более чем один отсчет и
гистограмма будет состоять из большого числа узких прямоугольников, почти
одинаковой высоты. Масштабы по осям гистограммы должны быть такими, чтобы
отношение её высоты к основанию примерно было равно 5:8.
5.Определяем границы
интервалов между выбранными бинами: 
6.Подсчитываем частоты
mi , равные числу результатов, лежащих в каждом i –
том интервале, т.е. меньших или равных его правой и больших
левой границы
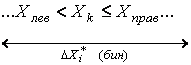
Этим правилом следует
руководствоваться, чтобы граничные результаты дважды не попали в соседние
бины.
6.Вычисляем частости,
представляющих собой статистические оценки вероятностей попадания
результатов измерения в i – интервал
(1.21)
где n –
общее число наблюдений, оставшихся после исключения “промахов.”
7.Если теперь разделить
частости на длину интервала,то получим величины, являющиеся оценками средней
плотности распределения в интервале 
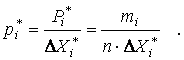(1.22)
Полученные
результаты следует свести в следующую табл.№1.3.
Таблица
№1.3.
|
№ |
|
|
|
Вариац. ряд |
Границы бинов |
№№ бинов |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
m1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
mr |
|
|
|
n |
|
|
|
|
|
|
|
|
|
8.Откладываем вдоль оси
абсцисс интервалы в порядке возрастания
индекса i и на каждом интервале строим прямоугольник с высотой равной
Полученный график (см.
рис.1.5.) называется гистограммой статистического распределения результатов
(ошибок) измерения.
Форма полученной
гисто-граммы позволяет сде-лать вывод о предпола-гаемом законе распре-деления
погрешностей измерения.
По форме гисто-граммы можно высказать предположение о “норма-льном”
(“гауссовском”), “равномерном”, “треуго-льном” или “законе арксинуса”(см.
раздел 1.4.3. настоящего пособия).
9.Определяем среднеквадратическое
отклонение среднеарифметических значений серии измерений
(1.23)
где
среднеквадратическое отклонение единичного ряда измерений,
найденное в пункте д).
среднеквадратическое
отклонение среднеарифметических значений серии k рядов по n
измерений одной и той же физической величины,
абсолютная погрешность каждого результата единичного ряда из n
измерений.
Примечание: Если бы производили k
серий
измерений одной и той же величины по n измерений в каждом
ряду, то полученные средне-арифметические значения 
имели бы некоторый разброс относительно матожидания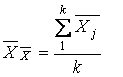 
этих среднеарифметических величин. При этом, как показано в
теории погрешностей, этот разброс в 
раз меньше разброса
отдельных измерений от среднеарифметического значения единичного ряда
измерений.
10.Записываем результат измерения (если n<50)
в следующем виде
(1.24)
где 
коэффициент Стъюдента, зависящий от количества измерений n и
заданной доверительной вероятности P, выбирается по
таб.№1.4. [3, 64]
Таблица
№1.4.
|
n |
P=0,95 |
P=0,99 |
n |
P=0,95 |
P=0,99 |
|
3 |
3,182 |
5,841 |
16 |
2,120 |
2,921 |
|
4 |
2,776 |
4,604 |
18 |
2,101 |
2,878 |
|
5 |
2,571 |
4,032 |
20 |
2,086 |
2,845 |
|
6 |
2,447 |
3,707 |
22 |
2,074 |
2,819 |
|
7 |
2,365 |
3,499 |
24 |
2,064 |
2,797 |
|
8 |
2,306 |
3,355 |
26 |
2,056 |
2,779 |
|
9 |
2,262 |
3,250 |
28 |
2,048 |
2,763 |
|
10 |
2,228 |
3,169 |
30 |
2,043 |
2,750 |
|
12 |
2,179 |
3,055 |
8 |
1,960 |
2,576 |
|
14 |
2,145 |
2,977 |
|
|
|
Литература.
1.Бурдун Г.Д.,Марков Б.Н. Основы метрологии. Учебное пособие для вузов. − М.: Изд-во стандартов, 1985.
2.Дворяшин
Б.В. Основы метрологии и радиоизмерения.– М.: Радио и связь,
1993.−
320 с.
Дисциплина:
«Метрология, стандартизация и сертификация»
Методические
указания к контрольным заданиям по теме:
Осциллографические измерения
(графические построения фигур Лиссажу, Задание 2)
Пример
(Вариант № 9): На пластины X и Y
электронно-лучевой трубки поданы напряжения u x(t)
и u y(t). Считая чувствительность X и Y пластин
одинаковой, графически построить траекторию луча при u y(t) = Um∙Cos(ωt+φ),
где φ = 900;
u x(t)
= UmCos(ωt).
Решение:
1.В
соответствии с принципом действия осциллографа [1,175] изображение на
экране электронно-лучевой трубки появляется в результате одновременного
действия на электронный луч двух взаимно перпендикулярных электрических полей,
создаваемых напряжениями на отклоняющих пластинах. Эти интерференционные
кривые получили название фигур Лиссажу. Для графического построения этих
кривых ортогонально располагают «временные» графики напряжения на пластинах «Y» (рис.1,б) и на пластинах
«Х» (рис.1,в), а пересечение «временных» осей позволяет определить центр экрана
ЭЛТ.
2. По формуле приведения [2,
182] u y(t) = Um1 = Cos(ωt+900)
= −UmSin(ωt). Графическое изображение
этой функции приведено на рис.1,б.
Указание: 2.1.Для
изображения синусоиды, сначала, следует выбрать отрезок на оси ОХ,
соответствующий периоду Т1 (например, на рис.1,б отрезок L1 = 8 cм).
Затем, на этой оси следует нанести «временной масштаб» кратный периоду Т1
и «угловой масштаб» кратный 2π..
2.2.На «временной» оси графика напряжения на пластинах «Х» (рис.1,в) выбирают отрезок L2 = L1 (!) и наносят аналогичный «временной» и «угловой» масштабы. Равные отрезки позволяют графически изобразить электрические сигналы равных частот ω.
2.3.Если напряжения на пластинах
имеют разные частоты (например, в варианте №20 на пластине «Y» действует напряжение с
частотой 4ω , а на пластине «Х» − с частотой 5ω ), то на этих равных
отрезках L небходимо отложить (на рис 1,б) четыре периода T1, а (на рис 1,в)
пять периодов T2.
3.Изображение на экране ЭЛТ получают по дискретным точкам. Для этого необходимо выбрать шаг дискретизации по времени ∆T или по фазе ∆φ. Удобнее использовать угловую величину ∆φ. Для получения изображения полусинусоиды необходимо иметь не менее 5-ти точек (см.рис1,б). Если использовать только 3 точки (1, 3, 5), то соединив эти точки прямыми линиями получаем треугольную фигуру. Точки 2 и 4 позволяют выявить характерный изгиб синусоиды. Таким образом чем меньше шаг дискретизации, тем ближе «ломаная» кривая к форме синусоиды. Из рисунка видно, что шаг дискретизации не должен быть больше ∆φ = π/4. Для этого угла синус равен 0,707, поэтому на графиках проведены уровни равные 0,707 Um, которые позволяют находить дополнительные точки. Если частоты напряжений на пластинах не одинаковы, то шаг дискретизации выбирается на кривой с наибольшей частотой и применяется такой же величины к кривой с менньшей частотой. В результате число точек дискретизации на обоих диаграммах должно быть одинаково.
4.Дискретные точки нумеруются и проектируются на «экран ЭЛТ». Пересечение одноименных проекций дают точки искомой кривой (см.рис.1,а).
5.Правильность полученной кривой проверяется методом расшифровки фигур Лиссажу. Для этого необходимо полученную кривую «мысленно» пересечь взаимно перпендикулярными прямыми «X» и «Y» и подсчитать число точек пересечения nx и ny. Например, для эллипса (рис.1,а) nx = 2 (точки 4 и 2), а ny = 2 (точки 4 и 6). Тогда, в соответствии с известным соотношением nx∙fx = ny∙fy, [1,196], отношение частот fx/fy = 1, что совпадает с условием задачи. Для фигуры «горизонтальная восьмерка» на том же рисунке отношение частот равно 4/2 или 2/1.
Примечание:
на рис. 1,в преднамеренно допущена ошибка, которую следует обнаружить,
внимательно прочитав вышеприведенное указание.
T1 T1 а) б) L1,см = L2,см ∆φ1 =
∆φ2 в) T2 Рис.1
Список литературы.
1.Нефедов В.И., Хахин В.И.,
Федорова и др. Метрология и электро-радиоизмерения в телекоммуникационных
системах: Учебник для вузов.−М.: Высш.шк., 2001.− 383 с.
2. Бронштейн И.Н., Семендяев К.А. Справочник по математике.
− М.: Гос.тех издат, 1974.−.608 с.
3.Графический редактор − «Advanced
Grapher 2.08».
Перечень вопросов по дисциплине “Метрология, сертификация и технические
измерения”-Рейтинг-1 этап.
1.Средства измерений (мера, первичный измерительный преобразователь, изме-
рительный прибор).[1, стр.30-32]
______________________________________________________________________
2.Классификация измерительных приборов по форме представления результата
измерения и по характеру измерений.[1, стр.33-38]
3.Преобразователи приборов прямого действия и приборов сравнения. Структур-
ные схемы и коэффициенты преобразования.[4, стр.45-48]
4.Метрологические характеристики: функция преобразования, чувствительность,
цена деления шкалы, порог чувствительности, вариация показаний.[1, стр.36-38,84-85]
5.Виды измерений: прямые, косвенные, совокупные и совместные.[1, стр.25-27]
6.Методы измерений: непосредственной оценки, сравнения, противопоставления,
дифференциальный, нулевой, замещения, совпадения.[1, стр.28-30, 2, стр.19-21]
7.Единицы измерений: основные, производные, внесистемные, кратные, дольные,
относительные.[3, стр.22-41, 1, стр.18-21]
8.Погрешности измерений: абсолютная, относительная, систематическая, случай-
ная, статическая, динамическая, основная, дополнительная,
приведенная.[1, стр.48-53]
_____________________________________________________________________
9.Аддитивная и мультипликативная погрешности измерения. Классы точности из-
мерения.[1, стр.84-90]
10.Характеристики случайных погрешностей: абсолютная погрешность, матема-
тическое ожидание, СКО, плотность вероятности, нормальный закон распределе-
ния случайных погрешностей.[1, стр.55-61, 2, стр.33-42]
11.Интегральная функция распределения случайных погрешностей, доверитель-
ная вероятность и доверительный интервал.[1, стр.55-61, 2, стр.33-42]
12.Обработка результатов прямых измерений с многократными наблюдениями.
Промахи и способ их исключения. Способ представления
результата измерений при большом и малом числе измерений. Коэффициент
Стъюдента.[2, стр.43-46, 1, стр.66-73]
_____________________________________________________________________
13.Суммирование погрешностей прямых и косвенных измерений.[1, стр.76-84]
14.Правила проверки согласия опытного распределения случайной погрешности с
теоретическим. Гистограмма.[3, стр.119-121, 2, стр.33-34]
15.Государственная система стандартизации. Цели, задачи и методы стандарти-
зации. Методы стандартизации (симплификация, унификация, типизация, агрега-
тирование ).[1, стр.306-313, 2, стр.174-179]
16.Виды и категории стандартов (ГОСТ, ОСТ, СТП ).Государственные системы стандартов (ЕДСКП, ЕСКД, ЕСТПП, ГСИ ).[1, стр.313-321, 329-334, 2, стр.180-182, 189-196]
17.Основы сертификации, варианты свидетельствования о
соответствии. Методы определения показателей качества.[1, стр.341-345, 2, 197-199]
______________________________________________________________________
Литература.
1.Нефедов В.И.,Хахин В.И.,Федоров Е.В. и др. Метрология и элекрорадиоизмере-
ния в телекоммуникационных системах:.Учебник для вузов.− М.: Высшая шк.,2001..
2.Тартаковский Д.Ф. ,Ястребов А.С. Метрология, стандартизация и технические измерений: Учеб.для вузов.− М.: Высш.шк.., 2001.
3.Бурдун Г.Д.,Марков Б.Н. Основы метрологии. Учебное пособие для вузов. − М.: Изд-во стандартов, 1985.
4.Кукуш В.Д. Электрорадиоизмерения. Учебн. пособие для вузов.− М.: Радио и связь, 1985.
Перечень вопросов
по дисциплине “Метрология, сертификация и технические
измерения”–Рейтинг–2 этап.
1.Аналоговые измерительные приборы. Уравнение измерительного механизма.
Момент количества движения, вращающий и противодействующий моменты и
момент успокоения. Амплитудно-частотная характеристика ИМ.[2, стр.68-70, 3,стр.109-113].
2.Измерительный прибор магнитоэлектрической системы. Принцип действия.
Уравнение угла отклонения подвижной части (уравнение шкалы) ИМ. Применение.[2, стр.68-74, 3, стр.113-120].
3.Измерительный прибор электромагнитной системы. Принцип действия. Урав-
нение угла отклонения подвижной части (уравнение шкалы) ИМ. Применение.
[2, стр.74-75, 3, стр.136-139].
4.Осциллографические измерения. Структурная схема осциллографа. Развертка
луча по горизонтали, синхронизация развертки. Коэффициент отклонения луча осциллографа по вертикали, коэффициент отклонения луча осциллографа по горизонтали.[1, стр.174-183, 2, стр.89-94, 3, стр.175-182].
5.Основные осциллографические измерения: амплитуды, частоты (двумя мето-
дами). Измерительные схемы и рассчетные формулы.[1, стр.194-197,198-200, 3, стр.413-417].
6.Основные осциллографические измерения: фазы электрических сигналов и характеристик транзистора или полупроводникового диода. Измерительная схема.[2, стр.119-122, 217-220, 3, 417-418].
7.Цифровые измерительные приборы. Способы дискретизации аналогового
сигнала (по уровню и по времени). Способ представления числа в десятичной и двоичной системе. Управляющие сигналы цифровой техники. Некоторые устройства цифровой техники: компаратор-“детектор нуля”, компаратор- “детек-тор уровня”, логический элемент “И” в качестве электронного ключа.[1, стр.95-112, 118-119, 3, 212-220, 235-236].
8.Цифровой вольтметр постоянного тока. Структурная схема и временные диаграммы преобразования аналогового сигнала в цифровой код. Уравнение
преобразования. Некоторые устройства цифровой техники: компаратор-“детек-
тор нуля”, компаратор- “детектор уровня”, логический элемент “И” в качестве
электронного ключа.[1, стр.140-147,2, стр.84-89].
9.Цифровые измерители частоты и периода. Структурные схемы и временные диаграммы преобразования аналогового сигнала в цифровой код. Уравнения преобразования.[1, стр.205-213]
10.Цифровой измеритель фазы электрических сигналов. Структурная схема и вре-
менные диаграммы преобразования аналоговой величины в цифровой код. Уравне
ния преобразования.[1, стр.222-228]
11.Мостовые методы измерения параметров элементов электрических цепей.
Условия равновесия мостовой схемы переменного тока. Особенности схем изме-
рения активных и реактивных сопротивлений.[1, стр.269-272, 3, стр.186-198]
Литература.
1.Нефедов В.И.,Хахин В.И.,Федоров Е.В. и др. Метрология и элекрорадиоизмере-
ния в телекоммуникационных системах.Учебник. М.: Высшая шк.,2001.
2.Тартаковский Д.Ф. ,Ястребов А.С. Метрология, стандартизация и технические измерения. М.,Высш.шк.,2001.
3.Авдеев Б.Я. и др.(под ред. Душина Е.М.).Основы метрологии и электрические измерения.Л.,Энергоатомиздат,1987.
3.3 Варианты заданий для
расчетно-графических работ
по дисциплине
«Метрология, стандартизация и сертификация».
Задание
1:
Произвести
статистическую обработку ряда наблюдений измеряемой величины с учетом объема
этого ряда. Выявить и исключить промахи в результатах наблюдений,
выдвинув (если возможно) гипотезу о законе распределения с заданной доверительной
вероятностью. Определить значение результата измерения, предполагая
отсутствие систематической погрешности. Определить случайную среднеквадратическую
погрешность результата измерения. Построить гистограмму результатов
наблюдений. Сделать вывод о правомерности выдвинутой ранее гипотезы.
|
Вари-ант |
Доверит. вероятн. |
Набор ряда наблюдений |
|
1 |
2 |
3 |
|
1 |
0.95 |
490, 501, 493, 495, 486,
450, 481, 486, 480, 463, 490, 520, 495, 492, 482, 518, 481, 505, 506, 508,
527, 492, 512, 512, 500, 501 |
|
2 |
0.95 |
393, 393, 395, 401, 409,
394, 405, 399, 384, 406, 383, 404, 388, 385, 423, 401, 396, 391, 391, 393,
423, 408, 407, 398, 415, 437 |
|
3 |
0.95 |
482, 502, 494, 497, 504,
489, 519, 492, 499, 461, 489, 559, 493, 491, 481, 510, 505, 490, 490, 502 ,
491, 476, 466, 506, 514, 522 |
|
4 |
0.95 |
513, 503, 516, 508, 495,
500, 490, 495, 491, 515, 522, 483, 527, 524, 504, 484, 479, 494, 504, 490,
529, 504, 514, 504, 521, 498, 533, 503, 496, 494 |
|
5 |
0.95 |
488, 495, 494, 496, 546,
498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505,
524, 509, 508, 493, 511, 518, 522, 503, 495, 500 |
|
6 |
0.95 |
287, 308, 290, 306, 296,
301, 291, 295, 290, 292, 290, 310, 304, 312, 324, 323, 318, 293, 293, 275,
275, 280, 269, 319, 297, 354 |
|
7 |
0.95 |
316, 307, 299, 291, 248
295, 315, 299, 304, 306, 314, 294, 268, 286, 309, 309, 303, 288, 288, 291,
290, 285, 275, 315, 302, 284, 335, 306, 278, 273, 300 |
|
8 |
0.95 |
267, 310, 292, 294, 342,
297, 307, 291, 286, 298, 286, 302, 313, 301, 281, 330, 325, 300, 280, 283,
282, 287, 294, 283, 291, 298, 312 |
|
9 |
0.95 |
304, 294, 326, 308, 306,
291, 281, 279, 281, 263, 291, 321, 295, 293, 283, 313, 307, 292, 290, 311,
310, 305, 315, 295, 283 |
|
10 |
0.95 |
297, 288, 310, 302, 343,
304, 275, 289, 284, 266, 320, 285, 319, 307, 297, 286, 281, 296, 306, 299,
328, 279, 290, 300, 307, 300 |
|
11 |
0.95 |
289, 309, 281, 304, 301,
316, 306, 308, 312, 314, 302, 292, 316, 324, 304, 294, 308, 303, 298, 307,
287, 331, 311, 301, 279, 276, 291, 311, 293, 293, 296, 292, 306, 314, 303 |
|
12 |
0.95 |
319, 299, 292, 314, 301,
296, 296, 311, 330, 309, 297, 297, 271, 289, 309, 288, 293, 318, 318, 296,
329, 304, 314, 314, 301, 308, 293, 303, 266, 281 |
|
13 |
0.95 |
385, 406, 388, 400, 408,
392, 413, 397, 392, 404, 386, 393, 368, 385, 405, 395, 390, 405, 405, 407,
386, 417, 410, 400, 388, 405, 380, 420, 402, 377 |
|
14 |
0.95 |
385, 406, 388, 400, 408,
392, 413, 397, 392, 404, 386, 393, 368, 385, 405, 395, 390, 405, 405, 407,
386, 417, 410, 400, 388, 405, 380, 420, 402, 377 |
|
15 |
0.95 |
297, 295, 271, 289, 309,
393, 394, 386, 408, 386, 411, 421, 385, 420, 412, 401, 401, 405, 403, 383, 423,
417, 392, 393, 375, 372, 389, 398, 398, 396 |
|
16 |
0.95 |
494, 505, 487, 489, 496,
501, 502, 578, 501, 467, 494, 524, 489, 496, 486, 506, 511, 486, 486, 506,
531, 506, 516, 506, 514, 526 |
|
17 |
0.95 |
319, 299, 292, 314, 301,
296, 296, 311, 330, 309, 297, 297, 271, 289, 309, 288, 293, 318, 318, 296,
329, 304, 314, 314, 301, 308, 293, 303, 266, 281 |
|
18 |
0.95 |
488, 495, 494, 496, 546,
498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505,
524, 509, 508, 493, 511, 518, 522, 503, 495, 500, 513 |
|
19 |
0.95 |
513, 503, 516, 508, 495,
500, 490, 495, 491, 515, 522, 483, 527, 524, 504, 484, 479, 494, 504, 490,
529, 504, 514, 504, 521, 498, 533, 503, 496, 494, 509 |
|
20 |
0.95 |
488, 495, 494, 496, 546,
498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505,
524, 509, 508, 493, 511, 518, 522, 503, 495, 500, 570 |
|
21 |
0.9 |
304, 294, 326, 308, 306,
291, 281, 279, 281, 263, 291, 321, 295, 293, 283, 313, 307, 292, 290, 311,
310, 305, 315, 295, 283, 305, 297 |
|
22 |
0.9 |
267, 310, 292, 294, 342,
297, 307, 291, 286, 298, 286, 302, 313, 301, 281, 330, 325, 300, 280, 283,
282, 287, 294, 283, 291, 298, 312, 303 |
|
23 |
0.9 |
316, 307, 299, 291, 248
295, 315, 299, 304, 306, 314, 294, 268, 286, 309, 309, 303, 288, 288, 291,
290, 285, 275, 315, 284, 335, 306, 278, 273, 300 |
|
24 |
0.9 |
287, 308, 290, 306, 296,
301, 291, 295, 290, 292, 290, 310, 304, 312, 324, 323, 318, 293, 293, 275,
275, 280, 269, 319, 297, 302, 354, 307 |
|
25 |
0.9 |
488, 495, 494, 496, 546,
498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505, 524,
509, 508, 493, 511, 518, 522, 503, 500 |
|
26 |
0.9 |
513, 503, 516, 508, 495,
500, 490, 495, 491, 515, 522, 483, 527, 524, 504, 484, 479, 494, 504, 490,
529, 504, 514, 504, 521, 498, 533, 496, 494 |
|
27 |
0.9 |
482, 502, 494, 497, 504,
489, 519, 492, 499, 461, 489, 559, 493, 491, 481, 510, 505, 490, 490, 502 ,
491, 476, 466, 506, 514, 522, 495, 503 |
|
28 |
0.9 |
393, 393, 395, 401, 409,
394, 405, 399, 384, 406, 383, 404, 388, 385, 423, 401, 396, 391, 391, 393,
423, 408, 407, 398, 415, 437, 407 |
|
29 |
0.9 |
490, 501, 493, 495, 486,
450, 481, 486, 480, 463, 490, 520, 495, 492, 482, 518, 481, 505, 506, 508,
527, 492, 512, 512, 500, 501, 505 |
|
30 |
0.9 |
488, 495, 494, 496, 546,
498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505,
524, 509, 508, 493, 511, 518, 522, 503 |
|
31 |
0.9 |
513, 503, 516, 508, 495,
500, 490, 495, 491, 515, 522, 483, 527, 524, 504, 484, 479, 494, 504, 490,
529, 504, 514, 504, 521, 498, 533, 503 |
|
32 |
0.9 |
488, 495, 494, 496, 546,
498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505,
524, 509, 508, 493, 511, 518, 522, 503 |
|
33 |
0.9 |
319, 299, 292, 314, 301,
296, 296, 311, 330, 309, 297, 297, 271, 289, 309, 288, 293, 318, 318, 296,
329, 304, 314, 314, 301, 308, 303, 266, 281 |
|
34 |
0.9 |
494, 505, 487, 489, 496,
501, 502, 578, 501, 467, 494, 524, 489, 496, 486, 506, 511, 486, 486, 506,
531, 506, 516, 506, 514, 526, 511 |
|
35 |
0.9 |
297, 295, 271, 289, 309,
393, 394, 386, 408, 386, 411, 421, 385, 420, 412, 401, 401, 405, 403, 383,
423, 417, 392, 393, 375, 372, 389, 398, 396 |
|
36 |
0.9 |
385, 406, 388, 400, 408,
392, 413, 397, 392, 404, 386, 393, 368, 385, 405, 395, 390, 405, 405, 407,
386, 417, 410, 400, 388, 405, 380, 420, 377 |
|
37 |
0.9 |
385, 406, 388, 400, 408,
392, 413, 397, 392, 404, 386, 393, 368, 385, 405, 395, 390, 405, 405, 407,
386, 417, 410, 400, 388, 405, 380, 420, 402 |
|
38 |
0.9 |
319, 299, 292, 314, 301,
296, 296, 311, 330, 309, 297, 297, 271, 289, 309, 288, 293, 318, 318, 296,
329, 304, 314, 314, 301, 308, 293, 303 |
|
39 |
0.9 |
289, 309, 281, 304, 301,
316, 306, 308, 312, 314, 302, 292, 316, 324, 304, 294, 308, 303, 298, 307,
287, 331, 311, 301, 279, 276, 291, 311, 293, 296, 303 |
|
40 |
0.9 |
297, 288, 310, 302, 343,
304, 275, 289, 284, 266, 320, 285, 319, 307, 297, 286, 281, 296, 306, 299,
328, 279, 290, 300, 307, 292, 306, 314, 300 |
|
41 |
0.99 |
500, 490, 495, 491, 515,
522, 483, 527, 524, 504, 484, 479, 494, 504, 490, 529, 504, 514, 504, 521,
498, 533, 496, 494 |
|
42 |
0.99 |
502, 494, 497, 504, 489,
519, 492, 499, 461, 489, 559, 493, 491, 481, 510, 505, 490, 490, 502 , 491,
476, 466, 506, 514, 522 |
|
43 |
0.99 |
393, 395, 401, 409, 394,
405, 399, 384, 406, 383, 404, 388, 385, 423, 401, 396, 391, 391, 393, 423,
408, 407, 398, 415, 437 |
|
44 |
0.99 |
490, 501, 493, 495, 486,
450, 481, 486, 480, 463, 490, 520, 495, 492, 482, 518, 481, 505, 506, 508,
527, 492, 512, 512, 500 |
|
45 |
0.99 |
495, 494, 496, 546, 498,
508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505, 524,
509, 508, 493, 511, 518, 522 |
|
46 |
0.99 |
516, 508, 495, 500, 490,
495, 491, 515, 522, 483, 527, 524, 504, 484, 479, 494, 504, 490, 529, 504,
514, 504, 521, 498, 533, 503 |
|
47 |
0.99 |
495, 494, 496, 546, 498,
508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505, 524,
509, 508, 493, 511, 518, 522, 503 |
|
48 |
0.99 |
299, 292, 314, 301, 296,
296, 311, 330, 309, 297, 297, 271, 289, 309, 288, 293, 318, 318, 296, 329,
304, 314, 314, 301, 308, 303, 266, 281 |
|
49 |
0.99 |
494, 505, 487, 489, 496,
501, 502, 578, 501, 467, 494, 524, 489, 496, 486, 506, 511, 486, 486, 506,
531, 506, 516, 506, 514, 526, 487, 489, 496 |
|
50 |
0.99 |
297, 295, 271, 289, 309,
393, 394, 386, 408, 386, 411, 421, 385, 420, 412, 403, 383, 423, 417, 392,
393, 375, 372, 389, 398, 396 |
|
51 |
0.99 |
392, 413, 397, 392, 404,
386, 393, 368, 385, 405, 395, 390, 405, 405, 407, 386, 417, 410, 400, 388,
405, 380, 420, 377 |
|
52 |
0.99 |
385, 406, 388, 400, 397,
392, 404, 386, 393, 368, 385, 405, 395, 390, 405, 405, 407, 386, 417, 410,
400, 388, 405, 380, 420, 402 |
|
53 |
0.99 |
319, 314, 301, 296, 296,
311, 330, 309, 297, 297, 271, 289, 309, 288, 293, 318, 318, 296, 329, 304,
314, 314, 301, 308, 293, 303 |
|
54 |
0.99 |
281, 304, 301, 316, 306,
308, 312, 314, 302, 292, 316, 324, 304, 294, 308, 303, 298, 307, 287, 331,
311, 301, 279, 276, 291, 311, 293, 296, 303 |
|
55 |
0.99 |
297, 288, 310, 302, 343,
304, 275, 289, 284, 266, 320, 285, 319, 307, 297, 286, 281, 296, 306, 299,
328, 279, 290, 300, 307, 292, 306, 314, 300 |
|
56 |
0.99 |
495, 494, 496, 546, 498,
508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505, 524,
509, 508, 493, 511, 518, 522, 503 |
|
57 |
0.99 |
494, 496,
546, 498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493,
505, 524, 509, 508, 493, 511, 518, 522, 503, 495, 500, 570 |
|
58 |
0.99 |
304, 294, 326, 308, 306,
291, 281, 279, 281, 263, 291, 321, 295, 293, 283, 313, 307, 292, 290, 311,
310, 305, 315, 295, 283, 305, 297, 300 |
|
59 |
0.99 |
267, 310, 292, 294, 342,
297, 307, 291, 286, 298, 286, 302, 313, 301, 281, 330, 325, 300, 280, 283,
282, 287, 294, 283, 291, 298, 312 |
|
60 |
0.99 |
308, 290, 306, 296, 301,
291, 295, 290, 292, 290, 310, 304, 312, 324, 323, 318, 293, 293, 275, 275,
280, 269, 319, 297, 302, 354, 307, 290, 310 |
|
61 |
0.95 |
316, 307, 299, 291, 248,
295, 315, 299, 304, 306, 314, 294, 268, 286 |
|
62 |
0.95 |
309, 309, 303, 288, 288,
291, 290, 285, 275, 315, 302 |
|
63 |
0.95 |
284, 335, 306, 278, 273,
300, 319, 299, 292, 314 |
|
64 |
0.95 |
488, 495, 494, 496, 546,
498, 508, 483, 477, 500, 487, 507, 497, 523 |
|
65 |
0.95 |
503, 493, 508, 502, 493,
505, 524, 509, 508, 493, 511, 518, 522, 503, 495 |
|
66 |
0.95 |
301, 296, 296, 311, 330,
309, 297, 297, 271, 289, 309, 288, 293, 318 |
|
67 |
0.95 |
318, 296, 329, 304, 314,
314, 301, 308, 293, 303, 266, 281 |
|
68 |
0.95 |
385, 406, 388, 400, 408,
392, 413, 397, 392, 404, 386, 393, 368, 385 |
|
69 |
0.95 |
405, 395, 390, 405, 405,
407, 386, 417, 410, 400, 405, 380, 420, 402, 377 |
|
70 |
0.95 |
386, 393, 368, 385, 405,
395, 390, 405, 405, 407, 386 |
|
71 |
0.95 |
385, 406, 388, 400, 408,
392, 413, 397, 392, 404 |
|
72 |
0.95 |
297, 295, 271, 289, 309,
393, 394, 386, 408, 386, 411, 421 |
|
73 |
0.95 |
417, 410, 400, 388, 405,
380, 420, 402, 377 |
|
74 |
0.95 |
385, 420, 412, 401, 401,
405, 403, 383, 423, 417, 392, 393 |
|
75 |
0.95 |
375, 372, 389, 398, 398,
396, 400, 401, 380 |
|
76 |
0.95 |
492, 482, 501, 506, 508,
504, 505, 506, 501 |
|
77 |
0.95 |
267, 310, 292, 294, 342,
297, 307, 291, 286, 298, 286, 302, 313, 301 |
|
78 |
0.95 |
281, 330, 325, 300, 280,
283, 282, 287, 294, 283, 291, 298, 312 |
|
79 |
0.95 |
490, 501, 493, 495, 486,
450, 481, 486, 480, 463, 490, 520, 495 |
|
80 |
0.95 |
482, 518, 481, 505, 506,
508, 527, 492, 512, 512, 500 |
Задание
2:
На пластины Y и X электронно-лучевой трубки поданы напряжения uy и ux. Считая чувствительность X и Y пластин одинаковой графически
постройте траекторию луча при: заданных uy и ux
.
|
вариант |
задание |
|
1 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=0° |
|
2 |
uy=Umcos(wt+j),
ux=Umcos2wt, при j=90° |
|
3 |
uy=Umcos(2wt+j),
ux=Umcoswt, при j=90° |
|
4 |
uy=Umcos(3wt+j),
ux=Umcos2wt, при j=90° |
|
5 |
uy=Umcos(wt+j),
ux=Umcoswt, при j= 45° |
|
6 |
uy=Umcos(wt+j),
ux=Umcos3wt, при j=90° |
|
7 |
uy=Umcos(3wt+j),
ux=Umcoswt, при j=90° |
|
8 |
uy=Umcos(2wt+j),
ux=Umcos3wt, при j=90° |
|
9 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=90° |
|
10 |
uy=Umcos(wt+j),
ux=Umcos4wt, при j=90° |
|
11 |
uy=Umcos(4wt+j),
ux=Umcoswt, при j=90° |
|
12 |
uy=Umcos(2wt+j),
ux=Umcos4wt, при j=90° |
|
13 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=135° |
|
14 |
uy=Umcos(4wt+j),
ux=Umcos2wt, при j=90° |
|
15 |
uy=Umcos(3wt+j),
ux=Umcos4wt, при j=90° |
|
16 |
uy=Umcos(4wt+j),
ux=Umcos3wt, при j=90° |
|
17 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=180° |
|
18 |
uy=Umcos(wt+j),
ux=Umcos5wt, при j=90° |
|
19 |
uy=Umcos(5wt+j),
ux=Umcoswt, при j=90° |
|
20 |
uy=Umcos(4wt+j),
ux=Umcos5wt, при j=90° |
|
21 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=225° |
|
22 |
uy=Umcos(5wt+j),
ux=Umcos4wt, при j=90° |
|
23 |
uy=Umcos(3wt+j),
ux=Umcos5wt, при j=90° |
|
24 |
uy=Umcos(5wt+j),
ux=Umcos3wt, при j=90° |
|
25 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=270° |
|
26 |
uy=2Umcos(wt+j),
ux=Umcoswt, при j=90° |
|
27 |
uy=Umcos(2wt+j),
ux=2Umcoswt, при j=90° |
|
28 |
uy=Umcos(wt+j),
ux=0.5Umcos2wt, при j=90° |
|
29 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=315° |
|
30 |
uy=2Umcos(wt+j),
ux=3Umcoswt, при j=90° |
|
31 |
uy=3Umcos(wt+j),
ux=2Umcoswt, при j=90° |
|
32 |
uy=3Umcos(wt+j),
ux=4Umcoswt, при j=90° |
|
33 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=60° |
|
34 |
uy=4Umcos(wt+j),
ux=3Umcoswt, при j=90° |
|
35 |
uy=4Umcos(wt+j),
ux=5Umcoswt, при j=90° |
|
36 |
uy=5Umcos(wt+j),
ux=4Umcoswt, при j=90° |
|
37 |
uy=Umcos(wt+j),
ux=Umcoswt, при j=120° |
|
38 |
uy=5Umcos(wt+j),
ux=3Umcoswt, при j=90° |
|
39 |
uy=3Umcos(wt+j),
ux=5Umcoswt, при j=90° |
|
40 |
uy=5Umcos(wt+j),
ux=2Umcoswt, при j=90° |
|
41 |
uy=Umcos(wt+j), ux=Umcoswt, при j=30° |
|
42 |
uy=Umcos(2pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
43 |
uy= Um - Um t / T, при 0 < t £
T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
44 |
uy= Um - 5 Um t / T, при 0 < t £ 0.2 T, uy = 5 Um (t-
0.2 T) / T, при 0.2
T< t £ 0.4 T и uy= 0 при 0.4 T< t £ T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
45 |
uy=Umcos(wt+j), ux=Umcoswt, при j=150° |
|
46 |
uy=Umsin(2pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
47 |
uy= Um t /
T, при 0 < t £ T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
48 |
uy=Um(сos(3pf t)+ sin(pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
49 |
uy=Umcos(wt+j), ux=Umcoswt, при j=210° |
|
50 |
uy=Umcos(3pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
51 |
uy=Umsin(4pf t+15°), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
52 |
uy=Um(сos(2pf t+60°)+ sin(pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
53 |
uy=Umcos(wt+j), ux=Umcoswt, при j=240° |
|
54 |
uy=Umsin(3pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
55 |
uy=Umsin(5pf t+60°), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
56 |
uy=Um(сos(4pf t+15°)+ sin(pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
57 |
uy=Umcos(wt+j), ux=Umcoswt, при j=330° |
|
58 |
uy=Umcos(4pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
59 |
uy=Umsin2(2pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
60 |
uy=Umcos(3pf t+60°), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
61 |
uy=Umcos2(3pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
62 |
uy=Umsin(4pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
63 |
uy=Umsin(3pf t+45°), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
64 |
uy=Umsin2(pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
65 |
uy= Um - Um
t / T, при 0
< t £
T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
66 |
uy=Umcos(5pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
67 |
uy=Umcos(2pf t+45°), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
68 |
uy=Umsin2(4pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
69 |
uy=Um(сos(2pf t+30°)+ 0.5 sin(pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
70 |
uy=Umsin(5pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
71 |
uy=Umcos2(2pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
72 |
uy=Umsin(2pf t+45°), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
73 |
uy= Um - 5 Um t / T, при 0 < t £ 0.2 T и uy = 1.25 Um (t- 0.5
T) / T, при 0.2 T<
t £ T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
74 |
uy=Umcos(6pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
75 |
uy=5 Um t /
T, при 0 < t £ 0.2 T и uy =Um - 1.25 Um (t- 0.5 T) / T, при 0.2 T< t £ T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
76 |
uy=Um(сos(pf t+30°)+ sin(2pf t)), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
77 |
uy= Um , при 0 < t £ 0.3 T, uy = 0, при 0.3 T< t £ 0.6 T, uy= 2 Um t / T
при 0.6 T< t £ T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
78 |
uy=Umsin(6pf t), f=1/T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
79 |
uy= Um - 2 Um t / T, при 0 < t £ 0.5 T и uy = 2 Um (t- 0.5 T) /
T, при 0.5 T< t £ T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
|
80 |
uy=2 Um t /
T, при 0 < t £ 0.5 T и uy =Um - 2 Um (t- 0.5 T) / T, при 0.5 T< t £ T ux=1.25 Um t / T, при 0 < t £ 0.8 T и ux=Um - 5 Um (t- 0.8 T) / T, при 0.8 T< t £ T |
Задание
3:
|
вариант |
задание |
|
1 |
Определите методическую
погрешность измерения тока в нагрузке 150 Ом амперметром с сопротивлением 10
Ом. |
|
2 |
Электронные весы c СКП 1%, построенные по
схеме прямого преобразования состоят из датчика веса с СКП 0.7% и цифрового
вольтметра. Определите СКП вольтметра. |
|
3 |
Определите СКП измерения
частоты 150 МГц цифровым методом, если СКП нестабильности частоты счетных
импульсов равна 10-6, а время счета 0.01 с. |
|
4 |
Определите методическую
погрешность измерения падения напряжения на сопротивлении 470 кОм, которое
подключено к генератору с внутренним сопротивлением 100 кОм, если вольтметр
имеет входное сопротивление 10 МОм. |
|
5 |
Выберите минимально
необходимую цену деления линейки, если СКО погрешности измерения длины
отрезка не должна превышать 0.5 мм, считая, что систематическая погрешность
равна нулю. |
|
6 |
Определите результат
косвенных измерений разности частот Df=f2–f1, где f1 и f2 – частоты, соответствующие границам полосы
пропускания и измеренные непосредственно частотомером. Результаты прямых
измерений: f1=304156
кГц, СКП sf1=0.30 кГц, систематическая
погрешность f1=f2=+0.8 кГц, f2=320394 кГц,
СКП sf2=0.32 кГц, считая
случайные погрешности некоррелированными. |
|
7 |
Определите число уровней
квантования и случайную погрешность АЦП, имеющего 24 двоичных разряда при СКП
нелинейности преобразования 0.0015%, считая погрешности квантования и
нелинейности случайными независимыми величинами. |
|
8 |
Оцените методическую
погрешность измерения амплитуды осциллографом с Rвх=1 Мом и Cвх=50 пФ, если
выходное сопротивление источника напряжения 4.7 кОм, емкость кабеля 5 пФ, а
частота сигнала 14 МГц. |
|
9 |
Погрешность вольтметра
характеризуется случайной (СКП 0.1 В) и систематической (+0.2 В)
составляющими. Найдите границы действительного значения напряжения с
доверительной вероятностью Р = 95 %, если вольтметр показал 15 В, считая, что
случайная погрешность распределена с нормальным законом распределения. |
|
10 |
Оцените погрешность
измерителя освещенности, построенного по схеме прямого преобразования и
содержащего фотодатчик с СКП 0.1%, измерительный усилитель с СКП 0.1% и аналоговый
вольтметр с СКП 1.5%. |
|
11 |
Оцените СКП измерения
временного интервала 0.1 с цифровым методом, если частота счетных импульсов
равна 10 МГц без учета нестабильности счетных импульсов, считая случайную
погрешность распределенной по треугольному закону. |
|
12 |
Цифровой вольтметр
класса точности 0.02/0.01 на пределе 10 В показал 7.248 В. Определите
абсолютное и относительное значение его погрешности. Какими будут его
погрешности на пределе 100 В. |
|
13 |
Оцените теоретическую
величину СКП формирования напряжения 10 разрядного ЦАП и сравните полученное
значение со справочными данными реального ЦАП 572ПА1. |
|
14 |
Емкость плоского
конденсатора определяется по формуле: C=e×eo×S/d, где eo=8.85×10-12 Ф/м,
e
- относительная диэлектрическая
проницаемость диэлектрика, S -
площадь пластин конденсатора, d -
расстояние между ними. Определите погрешность определения e по
измеренной емкости C,
если площадь пластин и расстояние между пластинами известны со случайными,
среднеквадратичными, независимыми погрешностями sS = 5 %
и sd = 7 %. |
|
15 |
Оцените методическую
погрешность измерения амплитуды напряжения частотой 10 МГц, если выходное
сопротивление источника напряжения 1кОм, осциллографом с Rвх=1 Мом и Cвх=50 пФ. |
|
16 |
Какая линейка более
точно позволяет измерить длину отрезка: с ценой деления 2.5 мм или 0.1 дюйма.
Почему? |
|
17 |
Оцените величину СКО
измерения напряжения идеальным АЦП с шагом квантования 10 мВ, считая, что
случайная ошибка распределена по треугольному закону. |
|
18 |
Определите результат
косвенного измерения сопротивления активной нагрузки по измеренному
напряжению 12 В, вольтметром класса точности 2.5 на шкале 30 В, и току 0.75
А, измеренному амперметром класса точности 1.5 на шкале 3 А. |
|
19 |
Оцените погрешность
измерителя перемещений, построенного по схеме прямого преобразования,
состоящего из индуктивного преобразователя перемещений с СКП 1% и аналогового
вольтметра с СКП 0.5%. |
|
20 |
К вольтметру класса
точности 1.5 с внутренним сопротивлением 30 кОм для расширения предела
подключен добавочный резистор 90±1 % кОм. Определите класс точности полученного
вольтметра. |
|
21 |
Определите число
наблюдений, необходимых для получения СКО оценки результата измерения 0.1 мВ,
если СКО одного наблюдения равна 0.5 мВ, считая, что погрешность вольтметра
распределена по нормальному закону. |
|
22 |
Определите число уровней
квантования и случайную погрешность АЦП, имеющего 20 двоичных разряда при СКП
нелинейности преобразования 0.002%, считая погрешности квантования и
нелинейности случайными независимыми величинами. |
|
23 |
Электронный уровень
(измеритель малых углов), построенный по схеме уравновешивающего
преобразования, содержит канал прямого преобразования с СКП 10% и канал
обратной связи с СКП 0.5%. Оцените погрешность уровня, считая, что
произведение коэффициентов передачи канала прямого преобразования и канала
обратной связи намного больше единицы. |
|
24 |
Погрешность вольтметра
характеризуется случайной (СКП 0.15 В) и систематической (-0.3 В)
составляющими. Найдите границы действительного значения напряжения с
доверительной вероятностью Р = 0.9, если вольтметр показал 24.7 В, считая,
что случайная погрешность распределена с нормальным законом распределения. |
|
25 |
Выведите формулу
определения методической погрешности измерения тока при известных:
сопротивлении амперметра и нагрузки. |
|
26 |
Оцените погрешность
измерения временных соотношений осциллографом с нелинейностью пилообразного
напряжения развертки не более 0.5%. |
|
27 |
Структурная схема
цифрового мультиметра содержит АЦП с СКП 0.05%, преобразователь сопротивления
в напряжение с СКП 4%, преобразователь тока в напряжение с СКП 0.01%,
детектор средневыпрямленных значений напряжения с СКП 2.5% и делитель
напряжений с СКП 0.05%. Нарисуйте его структурную схему и оцените его
погрешности в разных режимах работы, считая указанные погрешности
независимыми. |
|
28 |
Оцените погрешность
измерителя освещенности, построенного по схеме прямого преобразования и
содержащего фотодатчик с СКП 0.1%, измерительный усилитель с СКП 0.1% и
цифровой вольтметр с СКП 0.05%. |
|
29 |
Определите какой
результат измерения точнее: амперметром класса точности 1.5 со шкалой 3 А,
показывающим 0.82 А или амперметром класса точности 2.5 со шкалой 1 А,
показывающим 0.84 А. |
|
30 |
В каком диапазоне
измеряемых напряжений относительная погрешность вольтметра класса точности
0.02/0.01
на пределе 100 В не превысит 0.03 %. |
|
31 |
Определите с какой
точностью может измерять напряжение интегрирующий АЦП типа КР572ПВ5 и
определите оценку его СКП. |
|
32 |
Произведено 5 наблюдений
измеряемой величины: 511, 518, 522, 503, 495. Определить доверительный
интервал, в котором находится измеряемая величина, с доверительной
вероятностью 0.99. |
|
33 |
Оцените необходимое
время прогрева измерительного генератора, если его частота изменяется по
закону f(t)=fн+(f(0) - fн)exp(-t/t),
где fн=500 кГц - номинальная частота, f(0)=520 кГц -
частота в момент включения, t=4 мин - тепловая постоянная, если допустимая систематическая
погрешность частоты 1%. |
|
34 |
Определите погрешность
какого вольтметра при измерении напряжения 9.8 В меньше: класса точности 0.25
на пределе 10 В или класса точности 0.02/0.01 на пределе 100 В. |
|
35 |
Произведено 7 наблюдений
измеряемой величины: 385, 406, 388, 400, 408, 392, 413. Определить
доверительный интервал, в котором находится измеряемая величина, с
доверительной вероятностью 0.9. |
|
36 |
Оцените погрешность
аналогового электронного вольтметра, если в его составе аттенюатор-усилитель
с СКП 0.5%, детектор средневыпрямленного значения с СКП 1% и измерительный
механизм класса точности 0.5, считая указанные погрешности
некоррелированными. |
|
37 |
Оцените мощность,
рассеиваемую на динамике сопротивлением 4±1 Ом, если осциллограф,
подключенный к динамику показал двойной размах амплитуды синусоидального
сигнала 8.3 В, пренебрегая погрешностью осциллографа. |
|
38 |
Индуктивность контура L связана с резонансной
частотой wO и резонансной
емкостью СO соотношением L=1/(wO2×CO). Определить случайную
относительную погрешность измерения индуктивности gL по известным относительным
погрешностям частоты gw=0.1 % и емкости gС=0.2 %. |
|
39 |
Чему равна э.д.с.
генератора, если два вольтметра с входными сопротивлениями 10 и 20 кОм
показали значения 7.5 и 10 В соответственно. |
|
40 |
Выберите минимально
необходимую цену деления линейки, если СКО погрешности измерения длины
отрезка не должна превышать 1.5 мм, считая, что систематическая погрешность
равна нулю. |
|
41 |
Определите методическую
погрешность измерения тока в нагрузке 560 Ом миллиамперметром с
сопротивлением 710 Ом. |
|
42 |
Оцените СКП цифрового
вольтметра, имеющего 20000 уровней квантования на пределе 100 В, считая, что
случайная погрешность имеет треугольный закон распределения. |
|
43 |
Вольтметр с пределом 10
В и классом точности 1.0 показал 7.24 В. Определите абсолютное и
относительное значение его погрешности. |
|
44 |
Анализатор спектра имеет
полосу пропускания 30 кГц. Какое максимальное число спектральных линий он
может выделить в диапазоне частот от 10 до 110 МГц. |
|
45 |
Измерительный усилитель
содержит канал прямого усиления с К=100 при СКП 10% и цепь обратной связи с b=0.1
при СКП 1%. Найдите погрешность усилителя. |
|
46 |
Выведите формулу
определения входного сопротивления вольтметра по результатам двух измерений
напряжения U - без добавочного сопротивления, - с
известным добавочным сопротивлением |
|
47 |
Оцените величину СКО
измерения напряжения идеальным АЦП с шагом квантования 5 мВ, считая, что
случайная ошибка распределена по равномерному закону. |
|
48 |
По результатам прямых
измерений напряжения 12.5 В и сопротивления 613 Ом косвенно измерена мощность
постоянного тока. Определить величину мощности и СКП измерения, если известны
СКП прямых измерений: 0.03 В и 2 Ом. |
|
49 |
Последовательно соединены
10 резисторов номиналом 100 Ом с СКП 1%. Определите абсолютную и
относительную случайные погрешности такой сборки. |
|
50 |
Оцените погрешность
цифрового вольтметра, содержащего управляемый резистивный делитель напряжения
c СКП sД=0.1
% и АЦП с СКП sАЦП=0.05%,
считая эти погрешности некоррелированными. |
|
51 |
Определите число
наблюдений, необходимых для получения СКО оценки результата измерения 0.1 мВ,
если СКО одного наблюдения равна 0.25 мВ, считая, что погрешность вольтметра
распределена по нормальному закону. |
|
52 |
Погрешность вольтметра
характеризуется случайной (СКП 0.2 В) и систематической (+0.1 В)
составляющими. Найдите границы действительного значения напряжения с
доверительной вероятностью Р = 0.997, если вольтметр показал 9.8 В, считая,
что случайная погрешность распределена с нормальным законом распределения. |
|
53 |
Входное сопротивление
вольтметра равно 100 кОм. Как оно повлияет на погрешность измерения падения
напряжения в электронной схеме на эмиттерном сопротивлении величиной 1 кОм. |
|
54 |
Определите класс
точности амперметра (со шкалой 3 А), обеспечивающего измерение значения тока
0.82 А с погрешностью не больше, чем 0.01 А. |
|
55 |
Что покажет вольтметр
среднеквадратического значения напряжения при подаче на вход
последовательности двухполярных треугольных импульсов с частотой следования 7
кГц, если максимальный размах импульсов равен 3 В. |
|
56 |
Цифровым методом
измерения временного интервала проведено многократное наблюдение. Счетчик 45
раз зафиксировал 307 и 15 раз 308 счетных импульсов. Определите результат
измерения и СКП дискретизации, если шаг дискретизации равен 1 мкс, считая,
что счетные импульсы с временным интервалом не синхронизированы. |
|
57 |
Чему равен динамический диапазон, в дБ, цифрового
анализатора спектра на основе БПФ с 10 разрядным АЦП. Определите число
уровней квантования такого АЦП. |
|
58 |
Электронные весы c СКП 2.5%, построенные по
схеме прямого преобразования состоят из датчика веса с СКП 1.5% и цифрового
вольтметра. Определите СКП вольтметра. |
|
59 |
Определите СКП измерения
частоты 10 МГц цифровым методом, если СКП нестабильности частоты счетных
импульсов равна 10-6, а время счета 0.1 с. |
|
60 |
Определите методическую
погрешность измерения падения напряжения на сопротивлении 4.7 кОм, которое
подключено к генератору с внутренним сопротивлением 10 кОм, если вольтметр
имеет входное сопротивление 100 кОм. |
|
61 |
Определите результат
косвенного измерения потребляемой мощности по измеренному напряжению 12 В,
вольтметром класса точности 2.5 на шкале 30 В, и току 0.75 А, измеренному
амперметром класса точности 1.5 на шкале 3 А. |
|
62 |
Осциллограф показал
размах сигнала в контрольной точке 5 В. При включении щупа через
сопротивление 1.1 МОм величина размаха сигнала упала до 3 В. Определите
входное сопротивление осциллографа. |
|
63 |
По результатам прямых
независимых измерений емкости С1=394.7 пФ и С2=357.5 пФ определите разность
емкостей DС=С2-С1.
Определите предельную погрешность измерения емкости С, если известны
погрешности измеренных емкостей С2 и С1: систематические qc2=2.8 пФ, qc1=3.1 пФ и
случайные, подчиняющиеся нормальному закону распределения плотности
вероятности с СКП sс2=sс1=1.5
пФ. |
|
64 |
Что покажет вольтметр
среднеквадратических значений с открытым входом при подаче на его вход
последовательности однополярных прямоугольных импульсов с частотой следования
1 кГц и длительностью 10 мкс, если амплитуда импульса равна 1 В. |
|
65 |
Определите вероятность
превышения погрешности измерения ±40 мА, если в результате поверки амперметра
установлено, что 68% его измерений не превосходят ±20 mА, считая, что
погрешности распределены по норм. закону с нулевым мат. ожиданием. |
|
66 |
Оцените погрешность
измерения амплитуды напряжения осциллографом с неравномерностью АЧХ 0.15 дБ в
полосе пропускания. |
|
67 |
Образцовый динамометр с
СКП 0.01%, построенный по схеме прямого преобразования, состоит из вольтметра
с СКП 0.005% и тензодатчика. Оцените погрешность тензодатчика. |
|
68 |
Параллельно соединены 8
резисторов номиналом 1000 Ом, характеризующихся случайной,
среднеквадратичной, некоррелированной погрешностью ±10 %. Определите
абсолютную и относительную случайные погрешности такой сборки. |
|
69 |
Оцените инструментальную
ошибку измерения частоты пятью однотипными частотомерами в одинаковых
условиях: 148247, 148245, 148244, 148243, 148245 кГц. Определите результат
измерения и его СКП с доверительной вероятностью 95 %, считая, что случайные
погрешности отдельных приборов распределены по нормальному закону. |
|
70 |
В каком диапазоне
измеряемых напряжений относительная погрешность вольтметра класса точности
0.02/0.01
на пределе 10 В не превысит 0.03 %. |
|
71 |
Какой динамический
диапазон вольтметра позволит обеспечить используемый в нем 16 разрядный
идеальный АЦП. Определите число уровней квантования такого АЦП. |
|
72 |
На входы Y и X
осциллографа поданы напряжения Uy=sin(wt+j) и
Ux=sin(wt).
По размерам эллипса H и h определите разность фаз j, если H – это
максимальное отклонение по оси Y, а h – отклонение луча при x=0. Чему равна
СКП разности фаз, если H=4 см, h=3 см измерены с одинаковыми СКП sH=sh=1
мм. |
|
73 |
Оцените величину
временных искажений меандра (длительность фронта меандра) на экране
осциллографа, вызванных ограниченностью полосы пропускания осциллографа, если
его верхняя граничная частота равна 10 МГц. |
|
74 |
Для
магнитоэлектрического измерительного механизма с параметрами: магнитная
индукция в зазоре постоянного магнита равна 0.09 Тл, ток полного отклонения
0.1 мкА, число витков рамки 1200.5, средняя площадь рамки 4 см2,
длина витка 60 мм, диаметр медного провода 0.02 мм определите вращающий
момент полного угла отклонения стрелки и сопротивление рамки. |
|
75 |
При измерении временного
интервала счетчик цифрового прибора показал 50 раз 676 и 25 раз 675.
Определите величину временного интервала и СКП измеренного интервала, если
период счетных импульсов 1 мс, считая, что счетные импульсы синхронизированы
с началом временного интервала. |
|
76 |
Оцените величину
искажений передачи плоской части меандра (относительный спад вершины)
частотой 100 Гц на экране осциллографа, если его нижняя граничная частота
полосы пропускания равна 25 Гц. |
|
77 |
Структурная схема
цифрового мультиметра содержит АЦП с СКП 0.15%, преобразователь сопротивления
в напряжение с СКП 4%, преобразователь тока в напряжение с СКП 0.1%, детектор
средневыпрямленных значений напряжения с СКП 2.5% и делитель напряжений с СКП
0.05%. Нарисуйте его структурную схему и оцените его погрешности в разных
режимах работы, считая указанные погрешности независимыми. |
|
78 |
Определите границы
доверительного интервала при доверительной вероятности 0.68, если СКО
амперметра 0.05 А, при показании амперметра 1.57 А, считая, что случайная
погрешность амперметра распределена по нормальному закону. |
|
79 |
Мостовым измерителем
измерено сопротивление Rx=172.6
кОм. Оцените случайную погрешность измерения, если погрешности резисторов
моста не превышают 10-3. Запишите соотношение для Rx четырехплечего
моста постоянного тока. |
|
80 |
Определите величину
тепловой постоянной измерительного генератора, если изменение его частоты при
прогреве за 15 минут изменилась от 14980 до 15000 кГц, считая закон изменения
частоты экспоненциальным относительно номинального значения. |